Die Beurteilung dieser Ebene gestaltet sich aufgrund fehlender Testdaten beziehungsweise Testpersonen schwierig. Das zur Erstellung verwendete Modell ist in Anhang B nachzulesen. Nichtsdestotrotz können die erzielten Ergebnisse als gut bezeichnet werden. Die Antwortzeiten bewegen sich zwischen 0,1 und 0,2 Sekunden. Ausgehend von einer korrekten Wortkette (grammatisch korrekt und keine Erkennungsfehler) konnte in bezug auf die vorhandenen Modellsätze kein Fehler bei der Segmentierung in Chunks und der anschließenden Interpretation beobachtet werden, da alle Sätze in die Modellierung eingegangen sind. Selbst unter Mißachtung grammatikalischer Regeln konnte bisher kaum Fehlverhalten ermittelt werden. Selbst ein Satz wie ''Carl Kaffee Raum 6 mir'' kann umgesetzt werden. Bei Wortverdopplungen wie zum Beispiel in dem Satz ''Carl bring mir einen Kaffee in in Raum 6'' wird kein Kommando ausgelöst. Dies ist somit ein Fehler. Weitere Strukturen, die definitiv zu Interpretationsfehlern führen, sind bisher nicht bekannt.
Durch den Spracherkenner erzeugte Wortfehler führen möglicherweise zu Fehlern
in dieser Ebene. Nehmen wir an, die Fehlerrate des Spracherkenners auf Wortbasis
sei ![]() . Da einige Wörter in der Modellierung die gleiche semantische
Bedeutung erhalten haben, kann eine wortklassenbedingte Fehlerrate
. Da einige Wörter in der Modellierung die gleiche semantische
Bedeutung erhalten haben, kann eine wortklassenbedingte Fehlerrate ![]() mit dem Zusammenhang
mit dem Zusammenhang
![]() definiert werden. Die
definiert werden. Die ![]() -Relation
ergibt sich aus der Tatsache, daß bei der Klassenbetrachtung Erkennungsfehler
innerhalb einer Klasse keinen Interpretationsfehler nach sich ziehen. Die Klassen
ergeben sich aus den Definitionen der Heaps und Chunks (siehe 5.2.4
und Anhang B). Alle in einem Chunk oder einer Schlüsselwortmenge
verwendeten Wörter werden als bedeutungstragend bezeichnet. Weil die Wortklassen
nicht disjunktiv sein müssen, ist eine Bestimmung des exakten Wertes für
-Relation
ergibt sich aus der Tatsache, daß bei der Klassenbetrachtung Erkennungsfehler
innerhalb einer Klasse keinen Interpretationsfehler nach sich ziehen. Die Klassen
ergeben sich aus den Definitionen der Heaps und Chunks (siehe 5.2.4
und Anhang B). Alle in einem Chunk oder einer Schlüsselwortmenge
verwendeten Wörter werden als bedeutungstragend bezeichnet. Weil die Wortklassen
nicht disjunktiv sein müssen, ist eine Bestimmung des exakten Wertes für ![]() im Rahmen dieser Diplomarbeit zu aufwendig. Auch die Aussagekraft würde sich
in Grenzen halten, da das vorhandene Satzmaterial sehr begrenzt ist. Deswegen
wird im folgenden die oben angegebene Abschätzung verwendet. Ein Beispiel folgt
unten.
im Rahmen dieser Diplomarbeit zu aufwendig. Auch die Aussagekraft würde sich
in Grenzen halten, da das vorhandene Satzmaterial sehr begrenzt ist. Deswegen
wird im folgenden die oben angegebene Abschätzung verwendet. Ein Beispiel folgt
unten.
Nehmen wir an, daß alle Wörter unabhängig erkannt werden und ![]() bezeichnet die Wahrscheinlichkeit ein Wort korrekt zu erkennen. Dann ist
bezeichnet die Wahrscheinlichkeit ein Wort korrekt zu erkennen. Dann ist ![]() die Wahrscheinlichkeit,
die Wahrscheinlichkeit, ![]() Wörter richtig zu erkennen. Dann bezeichnet
Wörter richtig zu erkennen. Dann bezeichnet
die Wahrscheinlichkeit, mindestens ein Wort aus diesen ![]() Wörtern falsch
zu erkennen. Wir nehmen an, daß die Erkennung eines falschen Wortes bereits
zu einem Interpretationsfehler führt. In der Realität ist dies, durch die Definition
von Chunks und Heaps, nicht unbedingt zu erwarten.
Wörtern falsch
zu erkennen. Wir nehmen an, daß die Erkennung eines falschen Wortes bereits
zu einem Interpretationsfehler führt. In der Realität ist dies, durch die Definition
von Chunks und Heaps, nicht unbedingt zu erwarten.
Bei der Definition von ![]() sind wir davon ausgegangen, daß alle in
der Wortkette vorkommenden Wörter bedeutungstragend sind.
sind wir davon ausgegangen, daß alle in
der Wortkette vorkommenden Wörter bedeutungstragend sind. ![]() bezeichnet
im folgenden die Gesamtanzahl der Wörter eines Satzes und
bezeichnet
im folgenden die Gesamtanzahl der Wörter eines Satzes und ![]() die Anzahl
der bedeutungstragenden Wörter (Bedeutungslänge). Wir müssen nun noch den Fehler
betrachten, wenn ein nicht bedeutungstragendes Wort durch ein bedeutungstragendes
Wort substituiert wird. Die entsprechende Fehlerrate bezeichnen wir als
die Anzahl
der bedeutungstragenden Wörter (Bedeutungslänge). Wir müssen nun noch den Fehler
betrachten, wenn ein nicht bedeutungstragendes Wort durch ein bedeutungstragendes
Wort substituiert wird. Die entsprechende Fehlerrate bezeichnen wir als ![]() .
Da in der Realität eine deterministische Grammatik verwendet wird, tritt dieser
Fehler sehr selten auf beziehungsweise es handelt sich um einen Folgefehler
eines in
.
Da in der Realität eine deterministische Grammatik verwendet wird, tritt dieser
Fehler sehr selten auf beziehungsweise es handelt sich um einen Folgefehler
eines in ![]() enthaltenen Fehlers. Daraus folgt:
enthaltenen Fehlers. Daraus folgt:
![]() bezeichnet die Wahrscheinlichkeit mit der mindestens eins von
bezeichnet die Wahrscheinlichkeit mit der mindestens eins von ![]() nicht bedeutungstragenden Wörtern durch ein bedeutungstragendes ersetzt wird
und zu einer Fehlinterpretation führt. Es gilt:
nicht bedeutungstragenden Wörtern durch ein bedeutungstragendes ersetzt wird
und zu einer Fehlinterpretation führt. Es gilt:
Wenn ein nicht bedeutungstragendes Wort durch nicht bedeutungstragendes ersetzt
wird, so führt dies nicht zu einem Interpretationsfehler, da das Wort im Scanner
gefiltert wird. Daraus ergibt sich der Zusammenhang
wobei ![]() die Wahrscheinlichkeit einer Fehlinterpretation einer
Wortkette mit
die Wahrscheinlichkeit einer Fehlinterpretation einer
Wortkette mit ![]() Elementen, von denen
Elementen, von denen ![]() bedeutungstragend sind,
bezeichnet. Anders ausgedrückt ist es die Wahrscheinlichkeit, eines der
bedeutungstragend sind,
bezeichnet. Anders ausgedrückt ist es die Wahrscheinlichkeit, eines der ![]() bedeutungstragenden Wörter falsch zu erkennen. Wie an den gleich folgenden Berechnungen
zu sehen sein wird, ist der Wert von
bedeutungstragenden Wörter falsch zu erkennen. Wie an den gleich folgenden Berechnungen
zu sehen sein wird, ist der Wert von ![]() bei dem verwendeten Modell (siehe
Anhang B) nicht sehr groß. Weil zusätzlich
bei dem verwendeten Modell (siehe
Anhang B) nicht sehr groß. Weil zusätzlich ![]() nahe 0 ist, werden wir den Fehler
nahe 0 ist, werden wir den Fehler ![]() im folgenden wegen seines geringen
Werts (ebenfalls nahe 0) vernachlässigen. Damit folgern wir:
im folgenden wegen seines geringen
Werts (ebenfalls nahe 0) vernachlässigen. Damit folgern wir:
woraus wir ableiten:
Bei dieser Überlegung wird, wie oben gesagt, nicht betrachtet, daß einige Wortfehler keinen Einfluß auf die Fehlerrate haben. Dies ist zum Beispiel der Fall, wenn ein oder mehr nicht bedeutungstragende Wörter eingefügt werden (Insertions). Diese Wörter werden sowieso durch den Scanner gefiltert. Aber auch das Einfügen bedeutungstragender Wörter zieht nicht unbedingt einen Fehler nach sich. Ein Beispiel in bezug auf das verwendete Modell:
| Originalsatz: | Carl hol einen kaffee. |
|---|---|
| Fehlerhafter Satz: | Carl bitte hol mir einen kaffee. |
Das Wort mir ist bedeutungstragend und bitte nicht. Für Deletions
und Substitutions lassen sich ähnliche Fälle finden. Im folgendenden wird das
Verhältnis (![]() ) zwischen der durchschnittlichen Bedeutungs- (
) zwischen der durchschnittlichen Bedeutungs- (![]() )
und der durchschnittlichen Satzlänge (
)
und der durchschnittlichen Satzlänge (![]() ) als Abschätzung für die
Anzahl bedeutungstragender Wörter in einem Satz verwendet. Für das verwendete
Modell aus Anhang B ergeben sich die folgenden Werte:
) als Abschätzung für die
Anzahl bedeutungstragender Wörter in einem Satz verwendet. Für das verwendete
Modell aus Anhang B ergeben sich die folgenden Werte:
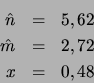
![]() bezeichnet im folgenden die Anzahl der Sätze der Länge
bezeichnet im folgenden die Anzahl der Sätze der Länge ![]() mit
mit ![]() bedeutungstragenden Wörtern.
bedeutungstragenden Wörtern. ![]() soll die Wahrscheinlichkeit
bezeichnen, mit der eine Wortkette der Länge
soll die Wahrscheinlichkeit
bezeichnen, mit der eine Wortkette der Länge ![]() mit
mit ![]() bedeutungstragenden
Wörtern auftritt. Unter der Annahme, daß alle Sätze gleich wahrscheinlich auftreten,
läßt sich
bedeutungstragenden
Wörtern auftritt. Unter der Annahme, daß alle Sätze gleich wahrscheinlich auftreten,
läßt sich ![]() berechnen durch:
berechnen durch:
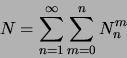
Dann kann die Fehlerrate des Parsers (![]() ) abgeschätzt beziehungsweise
deren obere Schranke (
) abgeschätzt beziehungsweise
deren obere Schranke (![]() ) berechnet werden durch:
) berechnet werden durch:
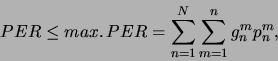
![]() sei die Wahrscheinlichkeit für das Auftreten einer Wortkette der
Länge
sei die Wahrscheinlichkeit für das Auftreten einer Wortkette der
Länge ![]() :
:
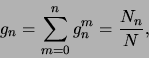
wobei gilt:
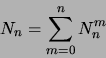
Durch die geringe Anzahl von Sätzen kann eine bessere statistische Aussagekraft
der Werte ![]() gegenüber
gegenüber ![]() bezweifelt werden. Die aus
dem Modell erhaltenen Werte können sich durch das Hinzufügen von wenigen Wortketten
stark verändern. Aus diesem Grund erscheint
bezweifelt werden. Die aus
dem Modell erhaltenen Werte können sich durch das Hinzufügen von wenigen Wortketten
stark verändern. Aus diesem Grund erscheint ![]() an dieser Stelle eine
genügend genaue Definition zu sein.
an dieser Stelle eine
genügend genaue Definition zu sein.
Mit obigen Abschätzungen
![]() und
und
![]() kann für die Fehlerrate des Parsers geschlossen werden:
kann für die Fehlerrate des Parsers geschlossen werden:

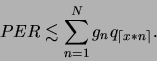
Es sei an dieser Stelle nochmals darauf hingewiesen, daß Wörtern die gleiche
semantische Bedeutung zugeordnet werden kann. Deshalb wäre für eine genauere
Bestimmung der Fehlerrate eine Einteilung in Wortklassen nötig. Daraus ergibt
sich die oben erwähnte Relation:
![]() . Als Beispiel sei hier
die Zuordnung von
. Als Beispiel sei hier
die Zuordnung von ![]() und
und ![]() zu einer Schlüsselwortmenge zu
nennen. Zusätzlich müßten die Fehlerarten (Insertions, Deletions und Substitutions)
genauer betrachtet werden. Eine Wortersetzung kann zum Beispiel weitreichendere
Folgen als eine Wortlöschung haben.
zu einer Schlüsselwortmenge zu
nennen. Zusätzlich müßten die Fehlerarten (Insertions, Deletions und Substitutions)
genauer betrachtet werden. Eine Wortersetzung kann zum Beispiel weitreichendere
Folgen als eine Wortlöschung haben.
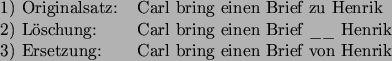
Der Sinn des zweiten Satzes kann mit dem vorliegenden System bestimmt werden, der des dritten Satzes nicht. In den Berechnungen wird aber davon ausgegangen, daß jeder Fehler die gleichen semantischen Konsequenzen nach sich zieht.
Die Berechnungen in Tabelle 6.1 machen deutlich, je mehr irrelevante Wörter
gegenüber bedeutungstragenden Wörtern in der Wortkette sind, desto höher ist
die Wahrscheinlichkeit, daß der Fehler bei einem irrelevanten Wort aufgetreten
ist. Die Spalte für ![]() kann für das implementierte Modell (siehe
Anhang B) als Anhaltspunkt dienen.
kann für das implementierte Modell (siehe
Anhang B) als Anhaltspunkt dienen.
Aufgrund der während einer Vorführung erhaltenen Daten (siehe 6.3.2) wurde eine PER von 27% errechnet. Dies impliziert eine ungefähre WER des Spracherkenners von 10%. Bei einer Fehlerrate des Spracherkenners von über 15% lassen sich eigentlich keine akzeptablen Ergebnisse des Gesamtsystems mehr erwarten.
| potentielle | max. PER in % | max. PER in % | max. PER in % |
| WER in % | |||
| 1 | 2,6 | 3,0 | 3,7 |
| 2 | 5,2 | 6,0 | 7,2 |
| 3 | 7,7 | 8,9 | 10,7 |
| 4 | 10,1 | 11,7 | 14,0 |
| 5 | 12,5 | 14,4 | 17,2 |
| 7,5 | 18,3 | 21,0 | 24,8 |
| 10 | 23,8 | 27,2 | 31,8 |
| 12,5 | 29,1 | 33,0 | 38,3 |
| 15 | 34,1 | 38,2 | 44,2 |
| 20 | 43,3 | 48,2 | 54,7 |