R3-[Q-Shape] - Research: Qualitative Spatial Reasoning
Basic Terms and Definitions
Binary Relations
Properties of Binary Relations
A binary relation R on a set X is a subset of ![]() , i.e. is a set of ordered pairs (x,y) with
, i.e. is a set of ordered pairs (x,y) with ![]() We will speak of R as a relation instead of
We will speak of R as a relation instead of ![]() . The collection of all binary relations on X will be denoted by Rel(X).
. The collection of all binary relations on X will be denoted by Rel(X).
Some important classes of binary relations over a set X are:
- reflexive:
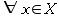 x in X it holds that xRx.
x in X it holds that xRx. - irreflexive:
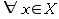 it holds that not xRx.
it holds that not xRx. - symmetric:
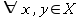 it holds that if xRy then yRx.
it holds that if xRy then yRx. - antisymmetric:
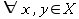 it holds that if xRy and yRx then x = y.
it holds that if xRy and yRx then x = y. - asymmetric:
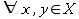 it holds that if xRy then not yRx.
it holds that if xRy then not yRx. - transitive:
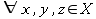 it holds that if xRy and yRz then xRz.
it holds that if xRy and yRz then xRz. - functional:
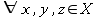 it holds that if xRy and xRz then y=z.
it holds that if xRy and xRz then y=z.
Operations on binary relations
If R is a binary relation over X, then each of the following are binary relations over X:
- Converse:
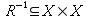 , defined as R-1 = { (y, x) |
, defined as R-1 = { (y, x) |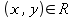 }. A binary relation over a set is equal to its converse if and only if it is symmetric. Sometimes the term reverse is used as well. The converse of a surjective and injective function is called its inverse.
}. A binary relation over a set is equal to its converse if and only if it is symmetric. Sometimes the term reverse is used as well. The converse of a surjective and injective function is called its inverse. - Reflexive closure: R=, defined as R=
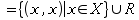 or the smallest reflexive relation over X containing R. This can seen to be equal to the intersection of all reflexive relations containing R.
or the smallest reflexive relation over X containing R. This can seen to be equal to the intersection of all reflexive relations containing R. - Transitive closure: R+, defined as the smallest transitive relation over X containing R. This can seen to be equal to the intersection of all transitive relations containing R.
- Transitive-reflexive closure: R*, defined as R* = ( R+) =.
If R, S are binary relations over X, then each of the following are binary relations:
- Union:
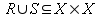 , defined as
, defined as 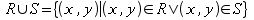 .
. - Intersection:
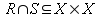 , defined as
, defined as 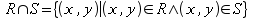 .
.
If R and S are binary relations over X, then the following is a binary relation over X as well:
- Composition:
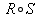 is defined as
is defined as 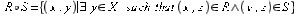 .
. - Weak composition:
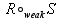 is defined as
is defined as 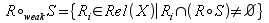 , or informally the strongest relation
, or informally the strongest relation 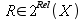 which contains
which contains 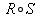 .
.
Ternary Relations
A ternary relation on a set X is accordingly a subset of X×X×X, i.e. is a set of ordered pairs <x,y,z> with x,y,z ∈ X.
Permutations
Because we have three arguments, we have 3! = 6 possible ways of arranging the arguments for a transformation. Following Zimmermann and Freksa [ZF96] the following terminology and symbols refer to these permutations of the arguments (a,b : c):
| term | symbol | arguments |
| identical | ID | a,b : c |
| inversion | INV | b,a : c |
| short cut | SC | a,c : b |
| inverse short cut | SCI | c,a : b |
| homing | HM | b,c : a |
| inverse homing | HMI | c,b : a |
An example for these binary operations can be found in [DM04].
Composition
With ternary relations, one can think of different ways of composing them. However there are only a few ways to compose them in a way such that it can be used for enforcing local consistency [SN01]. In the case of a real relation algebra, i.e. being closed under transformation and composition, e.g. the flip-flop calculus [IM99], we can enforce 4-consistency [IC00] using the following generalized scheme of strong composition ![]() [MN03]:
[MN03]: ![]()
Unfortunately, some calculi as for example the TPCC calculus is not closed under strong composition. For that reason we can not directly enforce 4-consistency. But we can define a weak composition operation ![]() of two relations r1 and r2. It is the most specific relation such that:
of two relations r1 and r2. It is the most specific relation such that: ![]() .
.
Bibliography
[DM04]: F. Dylla and R. Moratz. Emprical complexity issues of practical qualitative spatial reasoning about relative position. In Proceedings of the Workshop on Spatial and Temporal Reasoning, ECAI 2004, 2004.
[IC00]: A. Isli and A. Cohn, Qualitative spatial reasoning: A new approach to cyclic ordering of 2d orientation, Artficial Intelligence 122:137-187, 2000
[IM99]: A. Isli and R. Moratz, Qualitative Spatial Representation and Reasoning: Algebraic Models for Relative Position, TechReport Universität Hamburg FBI-HH-M-284/99 M-284, 1999
[MN03]: R. Moratz, B. Nebel, and C. Freksa, Qualitative Spatial Reasoning about Relative Position: The Tradeoff between Strong Formal Properties and Successful Reasoning about Route Graphs. Spatial Cognition 2003: 385-400, 2003
[SN01]: A. Scivos and B. Nebel, Double-Crossing: Decidability and Computational Complexity of a Qualitative Calculus for Navigation, Proc. COSIT-2001, Springer-Verlag, 2001
[ZF96]: K.Zimmermann and C. Freksa, Qualitative Spatial Reasoning Using Orientation, Distance, and Path Knowledge, Applied Intelligence, Volume 6, No.1, pp. 49-58, 1996.




