



Nächste Seite: GOLOG
Aufwärts: Das Situationskalkül
Vorherige Seite: Eine Lösung des Rahmenproblems
Inhalt
Fundamentale Axiome
-
![\( \forall P.P(S_{o})\wedge [\forall s\forall a.(P(s)\supset P(do(a,s)))]\supset \forall s.P(s); \)](img89.png)
-
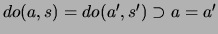

-

-
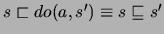 , mit
, mit
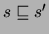 steht für
steht für
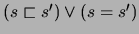
-
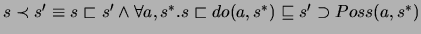
Die erste Aussage ist ein induktives Axiom zweiter Ordnung, das nur solche Situationen
zuläßt, die durch Anwendung von 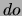 Termen aus
Termen aus 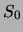 entstehen
können. Es wird also eine Baumstruktur mit den Situationen
entstehen
können. Es wird also eine Baumstruktur mit den Situationen 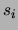 als
Knoten und den Aktionen
als
Knoten und den Aktionen 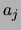 als Übergänge definiert. Das zweite Axiom
sichert die Eindeutigkeit des Übergangs von
als Übergänge definiert. Das zweite Axiom
sichert die Eindeutigkeit des Übergangs von 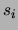 nach
nach 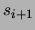 durch die Aktion
durch die Aktion 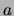 .
. 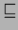 definiert eine geordnete Relation
über Situationen. Das dritte Axiom beschreibt also, daß es keine Vorgängersituation
vor der Situation
definiert eine geordnete Relation
über Situationen. Das dritte Axiom beschreibt also, daß es keine Vorgängersituation
vor der Situation 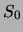 gibt.
gibt.
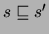 ist erfüllt, wenn
ist erfüllt, wenn
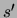 aus
aus 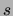 durch eine endliche Anzahl von Aktionen erreicht werden
kann. Zum Schluß gilt
durch eine endliche Anzahl von Aktionen erreicht werden
kann. Zum Schluß gilt 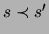 , wenn eine legale Sequenz (
, wenn eine legale Sequenz (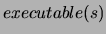 )
von Aktionen existiert, die von
)
von Aktionen existiert, die von 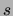 nach
nach 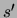 führt.
führt.
2001-01-04